Binäres Rätsel-Doodle für Alan Turing (inkl. Lösungen)

[Aktuell: George Boole Google Doodle] … Google feiert den „Erfinder“ der künstlichen Intelligenz Alan Turing mit einem coolen, interaktiven Doodle. Es hat ganz schön gedauert, bis ich das richtig durchschaut habe. Aber bei all dem technischen Schickschnack soll heute vor allem der 100. Geburtstag von Turing gewürdigt werden, der so viel für unsere heutige Zeit geleistet hat – und der dennoch so ein tragisches Leben führte.

Alan Turing war schwul. 1952 erfuhr die Polizei davon, als Turing einen Einbruch meldete. Er wurde verhaftet und wegen „grober Unzucht und sexueller Perversion“ verurteilt. Der Richter stellte ihn vor die Wahl: Gefängnisstrafe oder psychatrische Behandlung. Turing wählte letzteres. Im Rahmen der „Therapie“ wurden ihm Östrogene (weibliche Hormone) verabreicht, die dazu führten, dass ihm Brüste wuchsen. Turing wurde von Depressionen geplagt. 1954 nahm er sich im Alter von nur 41 Jahren das Leben, mit Hilfe eines vergifteten Apfels (als Junge hatte er ihn Schneewittchen fasziniert). Der (wahrscheinliche) Selbstmord wird seiner Depression zugeschrieben, auch wenn er nie bewiesen werden konnte, weil der Apfel entsorgt wurde. Im Jahre 2009 sagte der damalige britische Premier Gordon Brown: „We re sorry. You deserved so much better.“ („Es tut uns leid. Du hättest so viel Besseres verdient.“).
Der Mann, dem so viel Unrecht angetan wurde, hat jedoch so viel geleistet. Unsere heutige Welt wäre ohne Alan Turings Arbeit undenkbar. Geboren wurde Turing am 23. Juni 1912 in London. Schon früh zeigte sich seine hohe Intelligenz und außerordentliche mathematische Begabung. In der Schule wurde das allerdings nicht so recht deutlich, weil die Lehrer die Geisteswissenschaften wichtiger fanden. Es reichte dann aber doch für ein Mathematik-Studium in Cambridge.
Das Turing-Doodle
Doch kommen wir nun zum Doodle. Es ist ein interaktives Doodle, so eine Art Intelligenztest (für mich zumindest). Denn man muss erst mal darauf kommen, was zu tun ist. Und dann muss man noch das Prinzip verstehen, um die Rätsel zu lösen. Man beginnt das „Speil“, indem man auf den grünen Button klickt. Ziel ist es, die Google Buchstaben links oben mit Farben zu füllen. Rechts oben erscheint jeweils einen binärer Zahlencode, den nachbilden muss. Dafür muss man die Reihe mithilfe bestimmter „Methoden“ so programmieren, dass sie am Ende übereinstimmt. Anschließend prüft die Maschine die Zahlenfolge. Wenn es übereinstimmt, wir ein Buchstabe eingefärbt und die nächste Aufgabe erscheint. Hier die einzelnen Phasen des Turing-Doodles, inklusive Lösungen für die einzelnen Schritte…
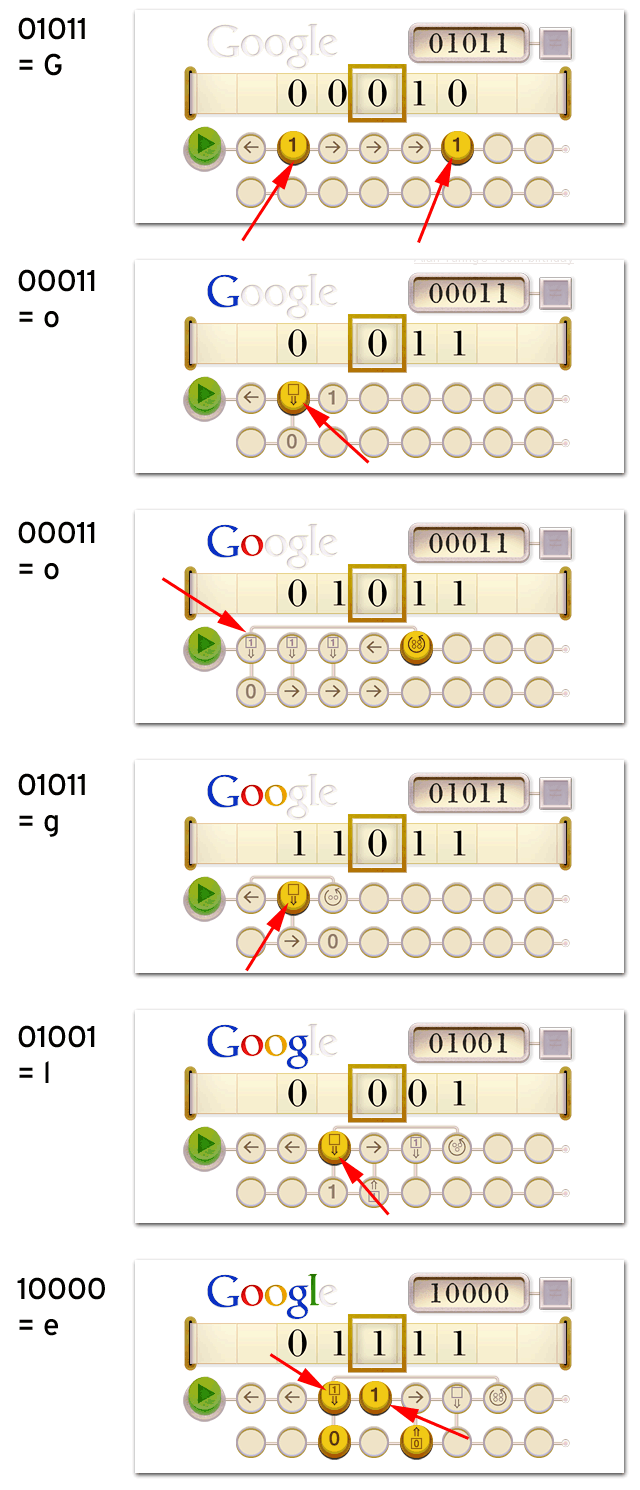
Übrigens sind die binären Zahlencodes computerbasierte Verschlüsselungen für unsere „Buchstaben„:
- 01011 = g
- 00011 = o
- 01001 = l
- 10000 = e
Turingmaschine und Enigma-Entschlüsselung
Zurück zu Turings Biografie: 1936 verfasste Turing die bahnbrechende Arbeit „On Computable Numbers, with an Application to the “Entscheidungsproblem”“ (sic!). Darin beschreibt er seine „Turingmaschine„. Ehrlich gesagt habe ich nicht verstanden, worum es genau geht. Es ist wohl theoretische Mathematik und hat damit zu tun, ob und wie man Dinge entscheiden kann (?). Auf jeden Fall ist es für die Entwicklung digitaler Systeme und damit für die Entwicklung der Computer wohl grundlegend. Wers kurz und bündig erklären kann: bitte gerne in den Kommentaren :-)
Im zweiten Weltkrieg entwickelte Turing eine mathematische Methode, mit deren Hilfe die von der deutschen Wehrmacht mittels „Enigma“ verschlüsselten Botschaften entschlüsselt werden konnten. Nicht wenige halten das für einen kriegsentscheidenden Schritt.
Interdisziplinäre Forschungen
Nach dem Krieg wandte er sich dann der Verknüpfung von Mathematik und Naturwissenschaften zu. In seinen Werk „The Chemical Basis of Morphogenesis“ ging es ihm um die Frage, wie man komplexe Beobachtungen aus dem Bereich der biologischen Entwicklung mathematisch fassen kann.
Das heutige Doodle ist mal wieder ein Meisterwerk von Google. Es ist dem Anlass entsprechend – dem 100. Geburtstag von Turing – passend. Aber es sollte auch dazu dienen, jede Form der Diskriminierung, und inbesondere den Vorurteilen gegenüber der Homosexualität, zu verurteilen. Wie würden die Geräte heute wohl aussehen, wenn Alan Turing seine geniale Arbeit hätte fortsetzen können. Übrigens ist Google in dem Bereich vorbildlich. Gebt mal ein: „gay pride“ – ein neues Google easter egg.
Hier wie immer das Doodle noch einmal als Video dokumentiert:
How to solve the ALAN TURING Google Doodle
Stanislaw Lem Doodle
Übrigens erinnert mich das Doodle in seiner Komplexität an das rästelhafte Doodle zu Ehren von Stanislaw Lem. Hier das entsprechende Lem-Doodle Video:
Mehr über Alan Turing
- Welt.de: Alan Turing – er knackte den Code der Wehrmacht
- Science-Blog: Alan Turing
- Turing.org (engl.): Alan Turing
- heise.de: Intelligenz ist ein soziales Produkt: Alan Mathison Turing zum 100. Geburtstag
- fokus.de: Google gratuliert Alan Turing mit interaktivem Doodle zum 100.
Weitere Artikel zum Turing-Doodle
- Putzlowitsch: Alan Turing zum 100. Geburtstag
- Oceparx: Alan Turing – Turingmaschine Google Doodle
- Seo-United: Alan Turing – Google Doodle für Mathematiker aus Großbritannien
- Infos über die Google Doodle-Zeichner
44 Gedanken zu „Binäres Rätsel-Doodle für Alan Turing (inkl. Lösungen)“
Wiederholt man das Spiel, gibt es neue Aufgaben, auf die die dargestellte Lösung nicht passt. Vielleicht solltest Du die Funktionsweise der Maschine beschreiben, das würde dem unbedarften Leser helfen auch andere Aufgaben zu lösen ;-) Da es Dein Blog ist, überlasse ich es Dir :-)
Danke. Bin gerade erst zurückgekommen und danke „huz“ (unten) dafür, dass er mir zuvorgekommen ist. :-)
Der wesentliche Punkt ist das Entscheidungsproblem – Turing hat damit das erste Mal eine »Maschine« beschrieben, die sich in Abhängigkeit von bestimmten Zuständen entscheiden kann, was sie als nächstes tut. ›Auf modern‹ heißt das »bedingte Verzweigung« – ohne die Algorithmen nicht Programme werden könnten. Damit konnte John von Neumann seine Architektur verwirklichen, der im Wesentlichen bis heute alle Computer folgen (Konrad Zuse entwickelte diese Architektur zur gleichen Zeit, schrieb es aber nicht auf).
Danke für den Hinweis.
Und wenn man nach Lösung aller Aufgaben auf das Häschen klickt, gibts noch ein e Überraschung…
aha, guter Hinweis. Muss ich gleich mal testen …
Das Entscheidungsproblem ist die Frage, ob es ein Programm geben kann, das ein beliebiges anderes Programm als Input bekommt und dann in endlicher Zeit entscheiden kann, ob das Input-Programm unendlich lange laufen würde, wenn man es ausführen würde, oder irgendwann zu einem Ende kommt.
Turing hat gezeigt, daß das nicht möglich ist. Es wird nie ein Programm geben können, dasfeststellen kann, ob ein beliebig anderes Programm in endlicher Zeit terminiert.
Eine andere, mehr praktisch relevante, Schlußfolgerung ist auch, daß es nie ein perfektes Antivirenprogramm geben können wird. Kein Programm kann jemals von einem beliebigen anderen Programm entscheiden können, ob es eine unerwünschte Funktion enthält.
Um noch tiefer in die mathematischen Hintegründe einzutauchen:
Man könnte natürlich eine Rechenmaschine, die diese Probleme nicht entscheiden kann für unvollständig halten. Dummerweise gibt es bis jetzt kein Rechenmodell, das mächtiger wäre (und es ist auch nicht zu erwarten, daß es überhaupt ein solches existieren kann). Von allen anderen Berechnbarkeitsmodellen wurde gezeigt, daß sie entweder genauso stark wie die Turingmaschine, oder schwächer sind. d.h. noch weniger Probleme entscheiden können. Im Informatikstudium lernt man beispielsweise ein Modell kennen, das noch nichteinmal entscheiden kann, ob von 3 verschiedenen Symbolen jeweils gleich viele auf einem Band stehen. Eine Turingmaschine (ein realer Computer ist genauso mächtig) kann das natürlich ohne Probleme entscheiden.
Und für die, die immer noch tapfer mitlesen hier die Beweiskizze für das Halteproblem:
Der Beweis wird als Widerspruchsbeweis geführt; d.h. man nimmt an, daß die Aussage die man beweisen will gilt, und leitet dann daraus einen logischen Widerspruch ab. Daraus folgt dann, daß die urspünglich angenommene Aussage falsch sein muß.
Angenommen es gibt ein Programm H, das in endlicher Zeit entscheiden kann ob ein beliebiges anderes Programm P irgendwann stoppen oder ewig weiterlaufen wird. Dann kann man ein Programm P‘ konstruieren, das H als Bestandteil besitzt und für den Fall, daß es die für sich selbst als Eingabe zum Ergebnis kommt: „P‘ hält in endlicher Zeit“ einfach in eine konstruierte Endlosscleife läuft.
Damit ist ein Widerspruch konstruiert. Die Annahme, daß ein Programm H exisitieren kann ist falsch.
öhem, Danke :-) wow…
Großartiger Artikel – unter mehreren Gesichtspunkten. Und Maschine hin, Maschine her, mich hat die Lebensgeschichte beeindruckt. Danke
LG – Elke
Das Doodle funktioniert eigentlich ganz einfach.
Sobald man den grünen Pfeil drückt werden einfach die 16 Kreise durchlaufen und die darinnen stehenden Aufträge ausgeführt.
-Ein Pfeil nach rechts bzw. nach links bedeutet dabei dass der Cursor sich nach rechts oder nach links bewegt.
-Eine 0 oder eine 1 trägt an der aktuellen Position des Cursors besagte Zahl ein.
-Der runde Pfeil mit den n Kreisen darinnen bedeutet einen Rücksprung um n Kreise.
-Und die Vierecke in dennen entweder nichts, eine 1 oder eine Null steht mit einem Pfeil darunter sind eine Verzweigung. Quasi wie ein if/else (Für jeden der sich ein bisschen mit Programmieren auskennt. :)).
Das ganze funktioniert so dass für den Fall das die Zahl am aktuellen Cursor der Zahl in dem Rechteck entspricht dann wird statt dem rechts liegenden Kreis als nächstes der darunter liegende ausgeführt.
Super beschrieben, Danke dafür :-)
„Übrigens sind die binären Zahlencodes computerbasierte Verschlüsselungen für unsere “Buchstaben““
sind sie gar nicht. Ein e wird nie als 10000 verschlüsselt, das macht keinen Sinn. Google hat diese Codes für die Buchstaben G, O, L, E für dieses Doodle „erfunden“!
Die letzte TM im zweiten Durchgang ist übrigens echt schwer :O
Hallo zusammen,
im Beitrag steht:
„Übrigens sind die binären Zahlencodes computerbasierte Verschlüsselungen für unsere “Buchstaben“: 01011 = g, 00011 = o, 01001 = l, 10000 = e“
Nach welcher Logik oder Zeichentabelle sind die Buchstaben codiert?
Viele Grüße // klingel
kann ich leider nicht sagen. Mir ist nur aufgefallen, das die „g“ und „o“ identisch sind.
Korrektur: die Darstellung der Buchstaben ist der für Fernschreiber verwendete Baudot-Code oder auch CCITT-2 oder ITA2.
Für Computer werden üblicherweise andere Codes verwendet, wie zum Beispiel ASCII oder Unicode
aha, Du hast Dich wohl sehr intensive mit dem Doodle beschäftigt. Danke für die Hinweise und Klarstellung.
noch was: wenn man am Ende oben rechts auf den Bunny klickt, kommt eine Turingmaschine, die die „Rabbit Sequence“ erzeugt
Endlich mal ein Doodle, an dem sich Geeks richtig austoben können. Nicht sowas wie Snake, woran alle Spaß haben :-D
Das Doodle war eine schöne Abwechslung.
Für alle „Normalos“ scheint es sich tatsächlich um ein „Rätsel“ zu handeln :)
Deine Artikel sind immer wieder faszinierend :) Eine sehr entscheidende, aber dennoch tragische Figur. Ein Opfer der damaligen Zeiten. Dass die Entwicklung damals so weit war, hätte ich nicht gedacht. Die Entschlüsselig der Botschaften war damals sicher kriegsentscheidend, das hatte ja enorme Vorteile. Aber interessant, wie huz das entschlüsselt hat, das ist einen Versuch wert :-)
Wiedermal ein sehr interessanter Artikel und danke für die Auflösung. Schon tragisch was den Genies in der Geschichte so widerfährt.
Hab diesen Artikel durch Zufall gefunden, schade, die Auflösung hätte ich gerne selber ausprobiert, zu spät… :-)
Ist doch logisch! Wie soll ein Programm oder ein System entscheiden können, ob es das gewünschte Ergebnis bringt, wenn es selbst nicht das Ergebnis kennt!
Gruß
Kommentare sind geschlossen.